The Official Homework Help Thread
- Thread starter Zandy
- Start date
The factors of any polynomial emanate their roots. Usually for factoring cubic polynomials you will first need to guess one of the roots of the equations to obtain an initial factor to work with. In this example, x = 1 is one such root (by trial and error), and so (x - 1) must appear as one of your factors.
You would then proceed by doing polynomial long division. You'd divide 4x^3 - 9x^2 + 6x - 1 by (x - 1). The result will be a quadratic polynomial which are much easier to factor. If you factor this quadratic polynomial, you will get the remaining terms!
There are other ways to factor more difficult cubic equations. For a cubic equation ax^3 + bx^2 + cx + d = 0, the roots are given by a cubic formula which is analogous to the quadratic formula but is much, MUCH more complicated:
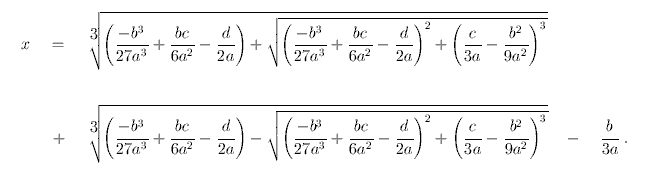
The factors of any polynomial emanate their roots. Usually for factoring cubic polynomials you will first need to guess one of the roots of the equations to obtain an initial factor to work with. In this example, x = 1 is one such root (by trial and error), and so (x - 1) must appear as one of your factors.
You would then proceed by doing polynomial long division. You'd divide 4x^3 - 9x^2 + 6x - 1 by (x - 1). The result will be a quadratic polynomial which are much easier to factor. If you factor this quadratic polynomial, you will get the remaining terms!
There are other ways to factor more difficult cubic equations. For a cubic equation ax^3 + bx^2 + cx + d = 0, the roots are given by a cubic formula which is analogous to the quadratic formula but is much, MUCH more complicated:
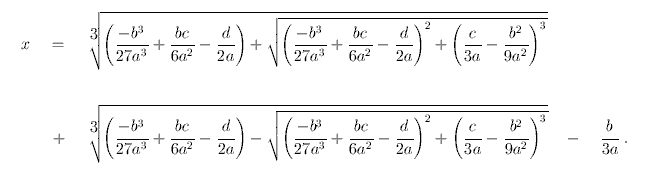
Oh god, this! Noooo! I always hated doing this! Anyways, thank you for the help! If I recall, you don't really guess right? Don't you have to find the factors of the constant term and then those are your possible roots? I might be wrong though.
DarkDesertFox
Your Typical Trickster
The factors of any polynomial emanate their roots. Usually for factoring cubic polynomials you will first need to guess one of the roots of the equations to obtain an initial factor to work with. In this example, x = 1 is one such root (by trial and error), and so (x - 1) must appear as one of your factors.
You would then proceed by doing polynomial long division. You'd divide 4x^3 - 9x^2 + 6x - 1 by (x - 1). The result will be a quadratic polynomial which are much easier to factor. If you factor this quadratic polynomial, you will get the remaining terms!
There are other ways to factor more difficult cubic equations. For a cubic equation ax^3 + bx^2 + cx + d = 0, the roots are given by a cubic formula which is analogous to the quadratic formula but is much, MUCH more complicated:
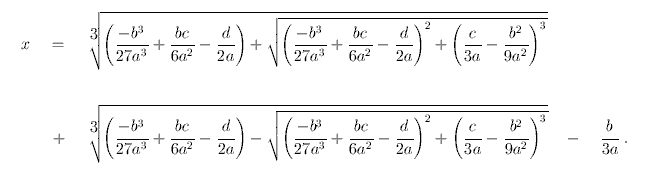
I'm in the top set and I don't understand
well its kinda guessing. like he said, u set
4x^3 - 9x^2 + 6x -1 = 0
then u "guess" values of x that hold true for that. and as he said, x = 1 is one of the solutions and therefore the factorised form must have a (x-1)...which u kno cuz the answer is (x-1)^2 (4x-1)
also are u told the answer? like does it give u the answer and ask u to write out the steps to solve it?
idk why zandy posted that cubic equation, all its doing is scaring and confusing ppl. its not needed for this problem
Last edited:
Yes, I understand that, but you would guess from the factors of -1 correct? Not just a random pool of numbers right?
well u guess like x = 1, 2, 3, -1, -2, -3 etc....its called factor theorem or something if u wanna look it up
There's some results regarding what the possible roots of polynomials can be depending on the coefficients/constant terms, though, I don't remember any of them so I couldn't be of much help xD. Those results are rather specialized cases though x).
T-that's not math. That's...
Haha, I know right xD? The one for the quartics is even scarier @_@... Here's just a subcase of the more general formulas xD:
To be honest, I don't know how to derive the equation either xP. It probably requires some pretty laborious algebra, haha
. It's rarely useful though because of how lengthy the formula is!
Mega_Cabbage
Meh
Which part do you need help with? Isn't it just a^2 + b^2 = c^2 where c is the hypotenuse?
Last edited:
Well I always have trouble figuring out what to do in a word problem with it, there is also a partw here you need to find b or a, like say "Johnny is going to paint his house, he gets on his ladder and starts. The side below the later is A and the hypotenuse is C, what's the answer?" Those problems.
Try to draw a diagram if you're not already given one. Then identify what you're given. If you need to solve for the hypotenuse then you're solving for c in a^2 + b^2 = c^2. If you need to solve for any other side then you're solving for a (or b, it doesn't matter how you label them).
Mega_Cabbage
Meh
It helps if you draw a picture. The side of the building and ground being lengths A and B. The ladder leaning on the building would be hypotenuse C. Plug it into the equation and solve for whichever variable you want to find.
id just like to point out that there's this question that hasen't been answered yet..
isnt it too late now rofl
